Solutions for lecture 14 exercises¶

    from matplotlib import pyplot as plt 
import numpy as np
from math import pi

Exercise 1: Crossover between extrinsic and intrinsic regimes¶

Question 1.¶

Law of mass action:

\[ n_e n_h = \frac{1}{2} \left(\frac{k_BT}{\pi\hbar^2}\right)^3 (m_e^{\ast}m_h^{\ast})^{3/2}e^{-\beta E_{gap}}\]

Charge balance condition:

\[ n_e - n_h + n_D - n_A = N_D - N_A \]

Question 2.¶

Since \(E_G \gg k_B T\), we can only use the law of mass action. But the question offers us another piece of information - we are around \(|N_D-N_A| \approx n_i\). That means that we are near the transition between extrinsic and intrinsic regimes. In this regime we can neglect \(n_D\) and \(n_A\) in this exercise, just like in the lecture. Writing \(n_e n_h = n_i^2\) and \(n_e - n_h = N_D - N_A\) and solving these together, we obtain

\[\begin{align*} n_{e} = \frac{1}{2}(\sqrt{D^2+4n_i^2}+D),\\ n_{h} = \frac{1}{2}(\sqrt{D^2+4n_i^2}-D) \end{align*}\]

where \(D = N_D - N_A\).

For \(n_i \gg |N_D - N_A|\) we recover the intrinsic regime, while the opposite limit gives the extrinsic expressions.

Question 3.¶

If \(D \ll n_i\), then the doping is not important and results of intrinsic are reproduced. Contrarily, if \(D \gg n_i\), it's mostly the doping that determines \(n_e\) and \(n_h\). The thermal factor becomes unimportant. Check both cases with lecture notes approximated solutions by doing a Taylor expansion.

Exercise 2: Donor ionization¶

Question 1.¶

If all the dopants are ionized (\(n_D \approx 0\)), the Fermi level is given by the expression for the extrinsic regime from the lecture.

Question 2.¶

The desired fraction is

\[ n_D = \frac{N_D}{\exp[(E_D-E_F)/k_B T]+1} \]

Question 3.¶

Using \(n_D \sim N_D\) we get

\[ (E_C - E_D)/k_B T \approx \log(N_C / (N_D - N_A)), \]

For germanium at room temperature \((E_C - E_D)/k_B T \approx 1/3\) (as derived in the lecture), and therefore as long as \(N_D - N_A \ll N_C \sim 1\%\), assuming that all donors are ionized is safe.

Exercise 3: Performance of a diode¶

Question 1.¶

Intrinsic semiconductors have no impurities. Adding dopant atoms creates extra unbounded electrons/holes depending on the n/p dopant atom added. Impurity eigenstates appear and the \(E_F\) level shifts (up/down for added donors/acceptors).

To make a diode a p-n junction is needed (extrinsic semiconductors). Drawing a diagram is very helpful.

Question 2.¶

Under reverse bias only two processes carry out current: electrons that may be thermally excited into the conduction band (p-doped side) and holes that may be thermally excited into the valence band (n-doped side).

Question 3.¶

\[ I_s(T) \propto e^{-E_{gap}/k_BT}\]

Exercise 4: Quantum well heterojunction in detail¶

Question 1.¶

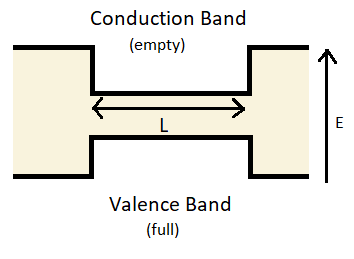
Include the energy bands here. You can find them at the book's section 18.2

Question 2.¶

This a "particle in a box" problem.

\[\begin{align*} -\frac{\hbar^2}{2m_e^{\ast}} \nabla^2 \Psi_e &= (E_e-E_c)\Psi_e\\ -\frac{\hbar^2}{2m_h^{\ast}} \nabla^2 \Psi_h &= (E_h+E_v)\Psi_h \end{align*}\]

Here and below \(E_h\) is the energy of a hole in the valence band.

Question 3.¶

\[\begin{align*} E_e = E_c + \frac{\hbar^2}{2m_e^{\ast}} ((\frac{\pi n}{L})^2+k_x^2+k_y^2),\\ E_h = -E_v + \frac{\hbar^2}{2m_h^{\ast}} ((\frac{\pi n}{L})^2+k_x^2+k_y^2) \end{align*}\]

Question 4.¶

This is a 2D electron/hole gas, therefore the DOS per unit area expression is the same as in 2D parabolic dispersion:

\[\begin{align*} g_e = \frac{m_e^{\ast}}{\pi\hbar^2},\\ g_h = \frac{m_h^{\ast}}{\pi\hbar^2} \end{align*}\]

Question 5.¶

\(L\) can be found here using previous questions, by setting:

\[ E_e + E_h - E_c + E_v = 1 eV = \frac{\hbar^2}{2}(\frac{\pi n}{L}^2+k_x^2+k_y^2) (\frac{1}{m_e^{\ast}}+\frac{1}{m_h^{\ast}}) \]

By choosing the correct \(n\), \(k_x\) and \(k_y\), \(L\) can be found as \(\approx 6.85\) nm

Question 6.¶

For a laser, one wants to fix the emission wavelength to a certain value. With this setup, the band gap is "easy" to design (set by \(L\), which is fixed).

Question 7.¶

If donor impurities are put outside of the well (on both sides, for example) the donated electrons can reduce their energies by falling into the well, but the ionized dopants remain behind. This gives an advanttage because an extremely high mobility for electrons can be obtained within the quantum well (there are no ionized dopants in the well to scatter off of). This is called modulation doping.